【Equations of Straight Lines DSE】直線方程｜囊括所有概念【全攻略】

Equations of Straight Lines 直線方程

直線是幾何學中最基礎、最常見的一種圖形，其具有許多獨特的特點和性質。
在數學中，我們可以使用各種不同的方法來描述直線，其中最常用的方法之一是直線方程。
直線方程可以通過幾何性質或代數方法來求解，並且可以描述直線在平面上的位置、傾斜角度、交點等重要特徵。
因此，對於想要深入了解幾何學和代數學的學生和研究者來說，學習直線方程是非常重要的一步。
在本篇文章中，我們將會介紹直線方程的基礎知識，包括斜截式、一般式等常用形式，並且深入探討直線方程在幾何學和代數學中的應用。

Equations of Straight Lines 直線方程 簡介

直線方程是描述平面上直線位置的數學公式。一條直線可以用不同形式的方程表示，但最常用的是一般式和斜截式。

一般式的方程形式為 Ax + By + C = 0，其中 A、B、C 為實數且 A 和 B 不同時，可以唯一地確定一條直線。可以通過將此方程中的 A 和 B 分別表示為斜率和方向角的正切值，得到直線的斜率和方向角。

斜截式的方程形式為 y = mx + b，其中 m 為直線的斜率，b 為直線在 y 軸上的截距，即當 x = 0 時，直線與 y 軸的交點的 y 坐標。

此外，也可以使用點斜式的方程來表示一條直線，該方程形式為 y – y1 = m(x – x1)，其中 m 為斜率，(x1, y1) 為直線上的已知點。

總之，直線方程是描述平面上直線位置的重要數學工具，它有多種形式，可以根據需要進行選擇和應用。

計算直線方程

直線方程可以用多種形式表示，以下是幾種常見的直線方程公式：

1. 一般式方程：Ax + By + C = 0，其中 A、B、C 為常數，A、B 不同時代表直線不平行於坐標軸，A=0時代表直線平行於 y 軸，B=0時代表直線平行於 x 軸。

2. 點斜式方程：y – y1 = m(x – x1)，其中 m 為斜率，(x1, y1) 為直線上的一點。

3. 截距式方程：y = mx + b，其中 m 為斜率，b 為直線與 y 軸的截距。

4. 兩點式方程：(y – y1)/(x – x1) = (y2 – y1)/(x2 – x1)，其中 (x1, y1) 和 (x2, y2) 為直線上的兩個點。

這些方程中，一般式方程較為通用，可以表示任何直線，但較不直觀；而點斜式和截距式方程較為常用，更容易理解和應用。兩點式方程則常用於求直線通過兩點的情況。

直線方程斜截式

直線的斜截式方程是一種常用的表示直線方程的形式，其中包含直線的斜率和截距。

斜截式方程的形式為 y = mx + b，其中 m 是直線的斜率，b 是直線在 y 軸上的截距。

斜率 m 表示直線在平面上的傾斜程度，計算方法為直線上任意兩點的高度差除以水平距離。如果直線向上傾斜，則斜率為正；如果向下傾斜，斜率為負；如果直線是水平的，則斜率為零；如果直線是垂直的，則斜率不存在（或稱為無限大）。

截距 b 表示直線與 y 軸的交點在 y 軸上的坐標。當 x = 0 時，直線的方程就是 y = b。

要求直線的 x 截距，可以使用斜率和 y 截距的值，通過將 y 替換為 0 來求得。

由於直線與 x 軸的交點的 y 坐標為 0，因此將 y 替換為 0，得到：

0 = mx + b

然後解出 x：

x = -b / m

因此，直線的 x 截距為 -b / m。注意，如果直線垂直於 x 軸，則斜率 m 為無限大或負無限大，此時 x 截距不存在。

斜截式方程提供了一種簡單而直觀的方式來描述直線的位置和方向。通過斜截式方程，我們可以直接讀出直線的斜率和截距，並從中推斷出直線的其他性質。

直線方程一般式

直線的一般式方程是另一種常見的表示直線方程的形式，它也可以描述直線的位置和方向。

一般式方程的形式為 Ax + By + C = 0，其中 A、B、C 是實數且 A 和 B 不同時，可以唯一地確定一條直線。這個方程可以看作是將斜截式方程中的 y 消去而得到的結果。

需要注意的是，一般式方程中的 A、B、C 可能不是最簡的，即它們有可能有公因數。在進行一般式方程的應用時，需要注意將 A、B、C 化簡為最簡的形式。

總之，一般式方程和斜截式方程是描述平面上直線位置的兩種常用形式，它們可以根據需要進行選擇和應用。

直線方程一般式 計算 x,y截距

可以使用直線的一般式方程 Ax + By + C = 0，來計算直線的斜率和截距。

首先，我們需要將一般式方程轉換為斜截式方程 y = mx + b 的形式。為此，我們可以求出斜率和截距的值：

1. 斜率 m = -A / B
   其中，A、B、C 是直線的一般式方程中的係數。需要注意的是，如果直線與 x 軸平行（即斜率不存在），則斜率 m 為無限大或負無限大。

   在直線的一般式方程 Ax + By + C = 0 中，斜率表示直線的傾斜程度，可以通過斜率的值來判斷直線是向上傾斜還是向下傾斜，以及傾斜的角度大小。
   直線的斜率可以通過一般式方程中的係數 A 和 B 來求得，公式為：
   斜率 m = -A / B
   需要注意的是，如果直線與 x 軸平行，則斜率不存在或者為無限大或負無限大；如果直線與 y 軸平行，則斜率為 0。如果直線是垂直於 x 軸或 y 軸的，則斜率不存在或者為無限大或負無限大。

2. y截距 = -C / B
   在直線的一般式方程 Ax + By + C = 0 中，y 截距是指直線與 y 軸的交點的 y 坐標，可以通過解出 y 軸上的點來求得。由於在 y 軸上，x 的坐標為 0，因此我們可以將 x 替換成 0，然後解出 y 的值。
   要求直線的 y 截距，可以將一般式方程中的 x 替換成 0，得到 By + C = 0。然後解出 y 的值：
   y = -C / B
   因此，直線的 y 截距為 -C / B。需要注意的是，如果 B = 0，則這條直線與 x 軸平行，不存在 y 截距。
3. x截距 = -C / A
   在直線的一般式方程 Ax + By + C = 0 中，x 截距是指直線與 x 軸的交點的 x 坐標，可以通過解出 x 軸上的點來求得。由於在 x 軸上，y 的坐標為 0，因此我們可以將 y 替換成 0，然後解出 x 的值。
   要求直線的 x 截距，可以將一般式方程中的 y 替換成 0，得到 Ax + C = 0。然後解出 x 的值：
   x = -C / A
   因此，直線的 x 截距為 -C / A。需要注意的是，如果 A = 0，則這條直線與 y 軸平行，不存在 x 截距。

綜上所述，使用直線的一般式方程可以計算出直線的斜率和截距。

理解兩直線相交的各種可能情況

兩條直線的相交情況可以分為以下幾種：

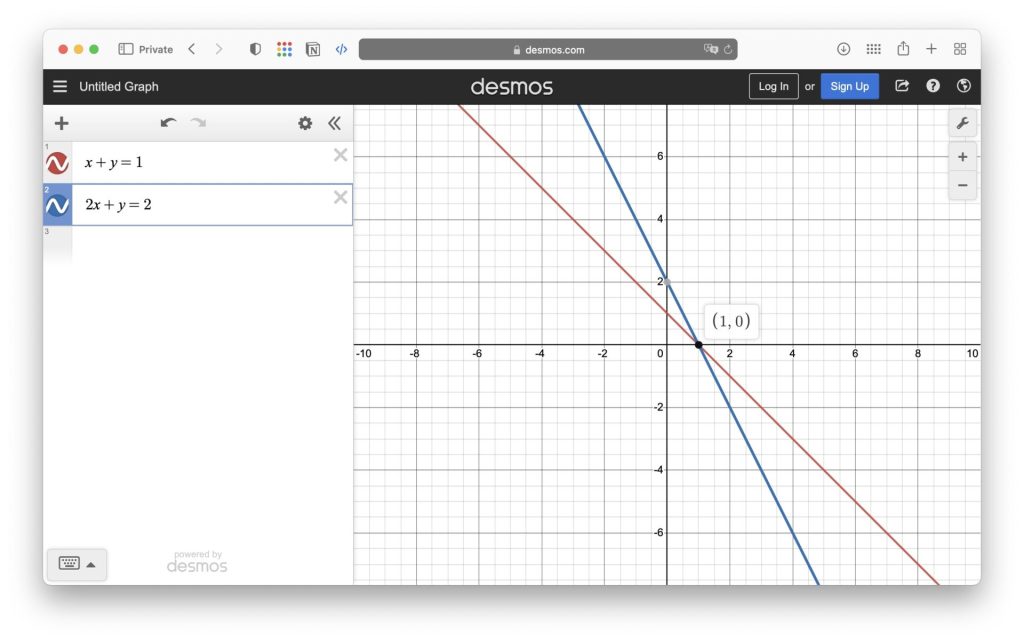
1. 相交於一點：兩條直線有一個且只有一個交點，這種情況是最常見的。

2. 平行：兩條直線沒有交點，且斜率相等，此時兩條直線平行於彼此。

3. 重合：兩條直線重疊在一起，有無限多個交點，且斜率相等且截距相等，此時兩條直線重合。

有一個交點

當兩條直線相交於一點時，它們的方程滿足以下特徵：

1. 兩條直線的斜率不相等，即它們的斜率互為相反數。如果兩條直線的斜率相等，它們將平行或重合，而不是相交。

2. 兩條直線的截距可以不同，但它們的截距差值不會超過交點的y座標。

3. 交點的座標可以通過解兩條直線的方程組來計算。假設兩條直線的方程分別為y = mx + b1和y = nx + b2，其中m和n為斜率，b1和b2為截距，則它們的交點的x座標可以通過求解方程mx + b1 = nx + b2來得到，交點的y座標可以通過將x座標帶入任一方程中計算得到。

4. 兩條直線的交點也可以用斜截式的公式來計算，斜截式的公式為y = mx + b，其中m為斜率，b為截距。如果兩條直線的斜率分別為m1和m2，截距分別為b1和b2，則它們的交點的x座標可以通過求解方程m1x + b1 = m2x + b2來得到，交點的y座標可以通過將x座標帶入任一方程中計算得到。

5. 假設直線方程1：A1x+B1y+C1 = 0
   假設直線方程2：A2x+B2y+C2 = 0
   如果兩條直線只有一個交點：
   A1/A2 ≠ B1/B2

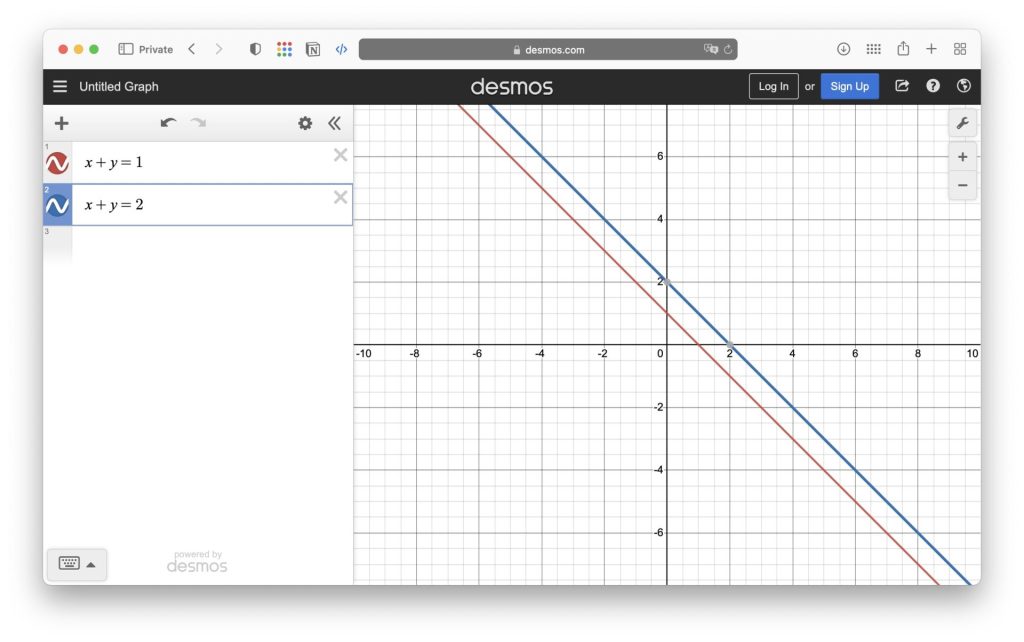
沒有交點 (兩線平行)

當兩條直線沒有交點時，它們的方程滿足以下特徵：

1. 由於兩條直線沒有交點，因此它們的解不存在，或者說解集為空。這時可以通過求解方程組得到矛盾的結果，比如0=1，這表示兩條直線永遠不會相交。

2. 由於兩條直線斜率相等，因此它們在坐標系中的位置關係固定不變，也就是說它們的位置關係是始終平行的。

3. 這時可以通過斜截式的公式來求解直線的位置和方向，斜截式的公式為y = mx + b，其中m為斜率，b為截距。由於兩條直線斜率相等，因此它們的截距可能不同，可以通過求解方程Ax + By = C來求得。

4. 假設直線方程1：A1x+B1y+C1 = 0
   假設直線方程2：A2x+B2y+C2 = 0
   如果兩條直線只有一個交點：
   A1/A2 = B1/B2 ≠ C1/C2

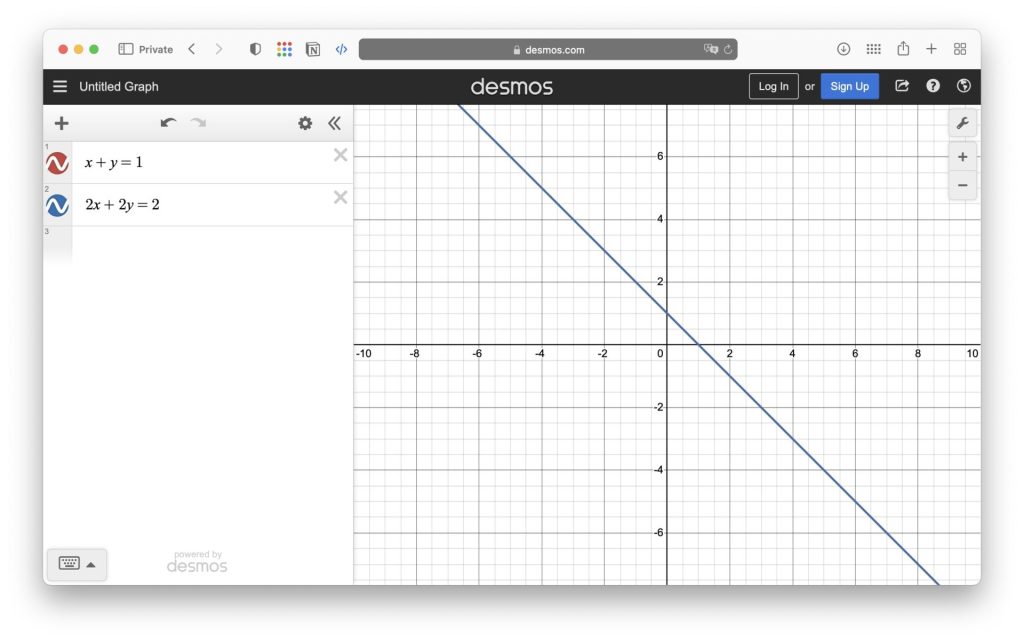
無限個交點 (兩線重疊)

當兩條直線有無限個交點時，它們的方程滿足以下特徵：

1. 兩條直線重合，因此它們在坐標系中的位置關係完全相同，位置、方向、斜率和截距等所有特徵都相同。

2. 由於兩條直線重合，因此它們的解是無數個，或者說解集為整個平面上的所有點。任意一個坐標為(x,y)的點都滿足Ax + By = C這個方程。

3. 這時可以通過斜截式的公式來求解直線的位置和方向，斜截式的公式為y = mx + b，其中m為斜率，b為截距。由於兩條直線重合，因此它們的截距相等，可以通過求解方程Ax + By = C來求得。

4. 假設直線方程1：A1x+B1y+C1 = 0
   假設直線方程2：A2x+B2y+C2 = 0
   如果兩條直線只有一個交點：
   A1/A2 = B1/B2 = C1/C2

直線方程 常見問題

斜率與傾角關係

斜率和傾角都是描述直線方向和傾斜程度的量，它們之間有以下的關係：

斜率是指直線上任意兩點的坡度，是直線上y軸方向的變化量除以x軸方向的變化量，斜率的計算公式為：m = Δy / Δx，其中Δy表示y軸方向的變化量，Δx表示x軸方向的變化量。斜率可以是正的、負的、零或不存在（無限大或無限小）。

傾角是指直線與x軸正方向的夾角，可以用反正切函數tan⁻¹(m)來計算，其中m是直線的斜率。由於反正切函數的返回值是弧度制，因此可以將其換算為角度制，也就是傾角。

具體來說，如果斜率是正的，則直線傾斜向右上方，其傾角在0度到90度之間；如果斜率是負的，則直線傾斜向左上方，其傾角在90度到180度之間；如果斜率為零，則直線水平，其傾角為0度；如果斜率不存在，則直線垂直，其傾角為90度。

如果大家有什麼補習問題，如私人補習、網上補習好唔好，歡迎你可以隨時再跟我多交流一下，可以Follow 「學博教育中心 Learn Smart Education」 Facebook page同IG得到更多補習課程資訊，亦都可以上我們的補習網頁了解更多!