【Exponential Functions DSE】指數函數｜帶你完全了解【完整指南】

Exponential Functions 指數函數

指數函數是高中數學中重要的一種函數，也是數學中常見的一種函數形式。
它以一個正實數為底數，以自變量的冪次形式表示，函數值為底數的冪次方。
指數函數在自然科學、工程技術、經濟學等領域中有廣泛的應用，是一種非常重要的數學工具。
本文將介紹指數函數的定義、性質、圖像特徵以及解指數方程的方法，幫助讀者深入理解這一重要的數學概念。

Exponential Functions 指數函數定義

exp函數

一般來說，指數函數的定義為：

f(x) = a^x

其中 a 是指數函數的底數，x 是指數。在這種情況下，指數函數的性質取決於底數 a 的取值。當底數 a 大於 1 時，指數函數是單調遞增的，當底數 a 在 0 和 1 之間時，指數函數是單調遞減的。

當底數 a 等於 1 時，指數函數為常數函數，即 f(x) = 1。當底數 a 小於 0 時，指數函數在某些情況下可能無定義或複數。

需要注意的是，指數函數以常數 e 為底數的情況被稱為自然指數函數或自然指數表達式，這是因為自然指數函數在很多數學和科學問題中具有特殊的地位和應用。

Laws of Rational Indices 有理指數的定律

有理指數的定律（Laws of Rational Indices）又稱指數定律（Laws of Exponents），是用來簡化涉及有理指數（指數表示為分數）的表達式的規則。

有理指數的三個主要定律如下：

1. 乘法法則：a^(m/n) * a^(p/n) = a^((m+p)/n)
   這意味著當兩個具有相同底數但指數不同的有理指數相乘時，可以將指數相加並保持相同的底數。
2. 除法法則：a^(m/n) / a^(p/n) = a^((m-p)/n)
   這意味著當兩個具有相同底數但指數不同的有理指數相除時，可以將指數相減並保持相同的底數。
3. 冪法則：(a^(m/n))^p = a^((m/n)*p)
   這意味著當將一個具有有理指數的項提高到另一個冪時，可以將指數乘以冪並保持相同的底數。

這些定律適用於任何底數（a）和任何有理指數（m/n和p/n），只要指數已定義且底數為正數。

這些定律在簡化和操縱涉及有理指數的表達式方面非常重要，可以用於解決涉及有理指數的各種數學問題。

理解有理數指數的定義

有理數指數是指指數是有理數的冪運算，即形如 a^(m/n) 的數，其中 a 是一個正實數，m 和 n 是整數且 n ≠ 0。

有理數指數的定義保證了指數運算在有理數集合內的封閉性。因為有理數是整數和分數的集合，而對於整數指數的冪運算，我們已經知道了其定義和性質，因此只需要將分數指數的冪運算定義為整數指數的冪運算的推廣，就可以保證指數運算在有理數集合內的封閉性。

具體地，設 a 是一個正實數，m 和 n 是整數且 n ≠ 0，定義 a^(m/n) 為 a^m 的 n 次方根，即 (a^m)^(1/n)。由於指數運算和根號運算是反函數關係，所以有理數指數的冪運算與整數指數的冪運算具有類似的性質，例如指數運算的結合律和分配律等。

總之，有理數指數的定義使得指數運算可以在更廣泛的數域內進行，並且保持了指數運算的基本性質，為更複雜的數學運算和應用提供了基礎。

Exponential Functions 指數函數性質

指數函數有以下的性質：

1. 定義域和值域：指數函數的定義域為實數集 R，值域為正實數集 {y|y>0}。
2. 增減性：當底數 a 大於 1 時，指數函數是增函數，即隨著自變量 x 的增加，函數值也隨之增加；當底數 a 在 0 和 1 之間時，指數函數是減函數，即隨著自變量 x 的增加，函數值卻隨之減少。
3. 對數函數的反函數性質：指數函數和對數函數是互為反函數的，即 y = a^x 和 x = log_a y 互為反函數。
4. 指數函數的極限：假設a > 0當 x 趨近於負無窮時，指數函數 f(x) = a^x 的極限為 0；當 x 趨近於正無窮時，指數函數的極限為正無窮。

這些性質使指數函數在數學和科學領域中有著廣泛的應用，例如在微積分、統計學、物理學、金融學等領域中都有著重要的作用。

指數函數圖像

指數函數的圖像具有以下特徵：

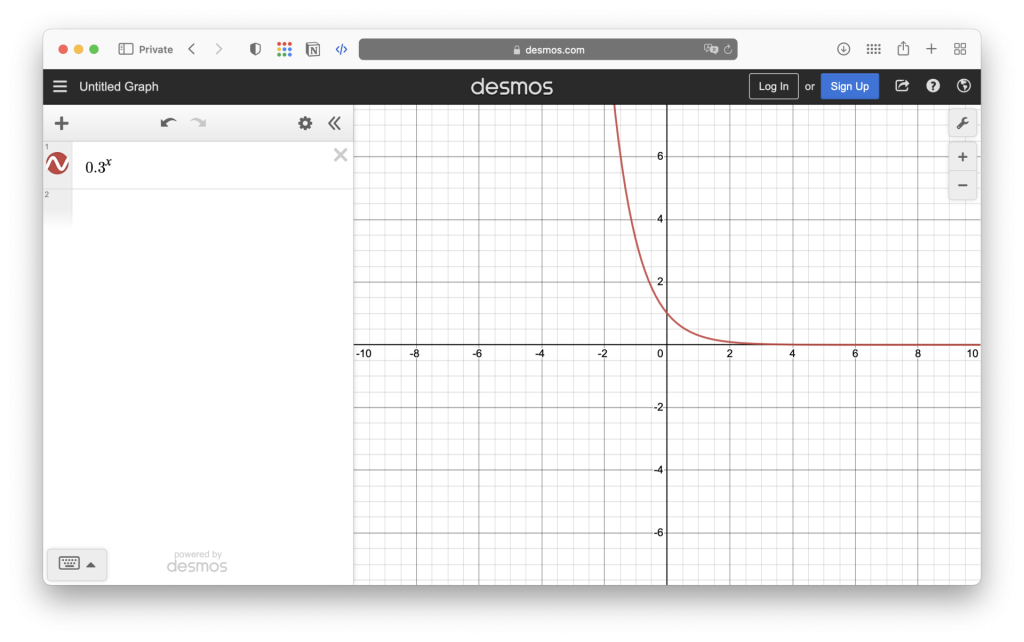
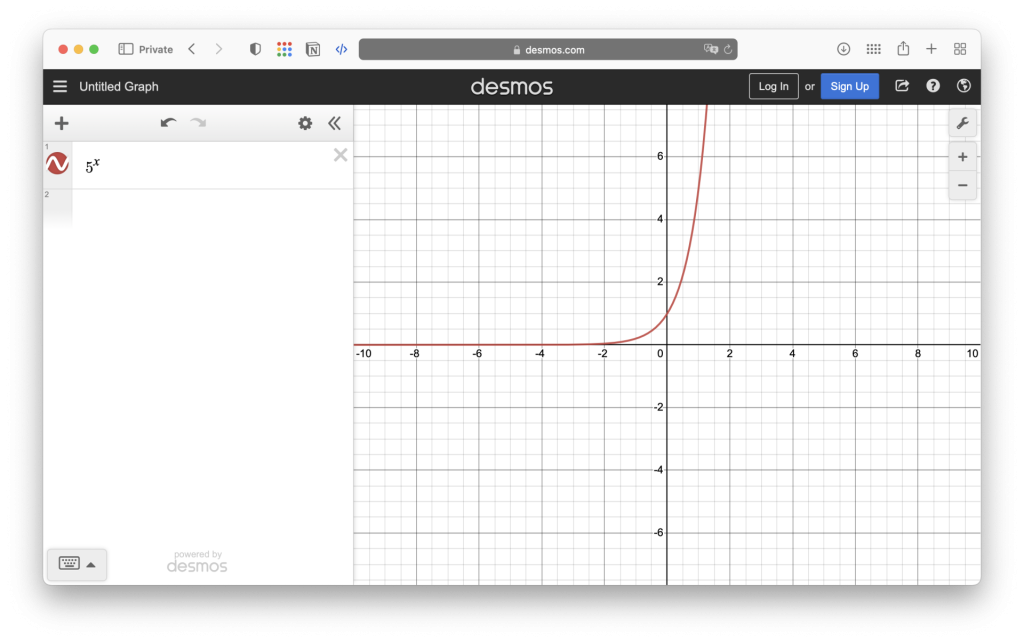
1. 基本形態：指數函數的一般形式為 f(x) = a^x，其中 a 為正實數，且不等於 1。當 a 大於 1 時，函數圖像隨著 x 的增加而上升；當 0 < a < 1 時，函數圖像隨著 x 的增加而下降。當 a 等於 1 時，函數圖像為一條水平直線 y = 1。
2. 共同y截距：f(x) = a^x，不論a是什麼都會有同樣的y截距 = 1
3. 定義域和值域：指數函數的定義域為實數集 R，值域為正實數集 {y|y>0}。
4. 漸近線：指數函數的漸近線為 x 軸，即當 x 趨近於負無窮時，函數值趨近於 0，而當 x 趨近於正無窮時，函數值趨近於正無窮。
5. 變化速率：指數函數在定義域內的變化速率與函數值成正比。當底數 a 大於 1 時，函數值隨著 x 的增加而增加，增長速度逐漸加快；當 0 < a < 1 時，函數值隨著 x 的增加而減少，衰減速度逐漸減緩。
6. 複合函數：指數函數可以與其他函數進行複合，例如與正弦函數、餘弦函數、指數函數等複合，可以得到更加複雜的函數圖像。

當底數為0至1之間

當底數大於1

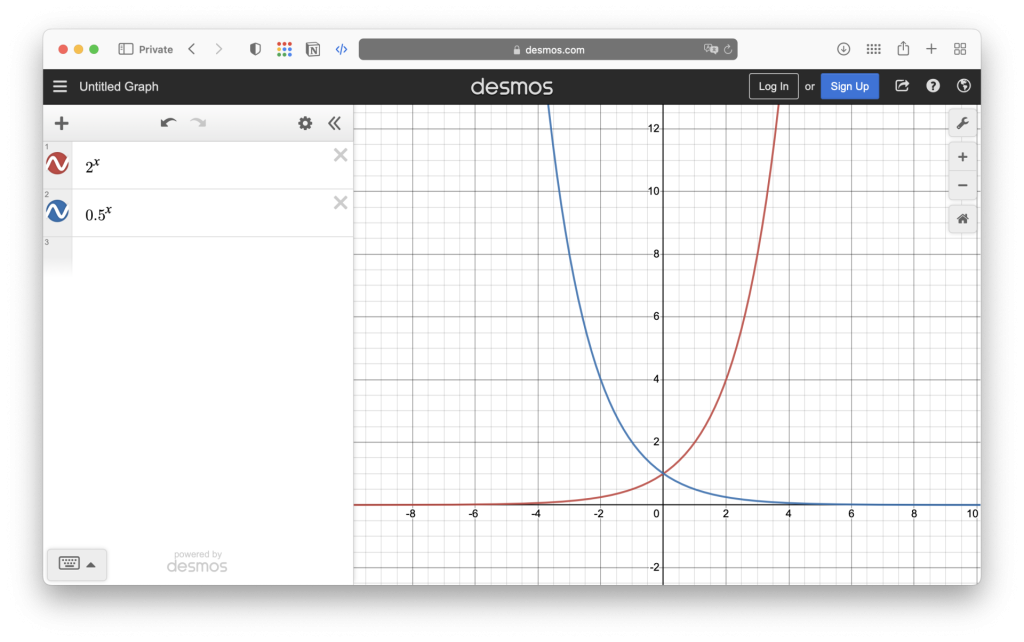
對稱性

對於指數函數 f(x) = a^x (a>0, a≠1)，當底數為 2 時，有 f(-x) = 2^(-x) = 1/2^x = 1/f(x)。

當底數為 0.5 時，有 f(-x) = (0.5)^(-x) = 2^x = 1/f(x)。

這些對稱性可以通過函數圖像進行直觀的理解和驗證。以底數為 2 的指數函數 f(x) = 2^x 為例，當 x=1 時，函數值為 f(1) = 2；當 x=-1 時，函數值為 f(-1) = 1/2。這意味著函數圖像上的點 (1,2) 和 (-1,1/2) 關於 y 軸對稱。同樣地，對於底數為 0.5 的指數函數，函數圖像上的對稱點也可以通過類似的方式得到。

解指數方程

指數方程是形如 a^x = b 的方程，其中 a 和 b 是常數，而 x 是未知量。要解決這種方程，可以使用以下方法：

對數法：將指數方程轉化為對數方程。如果 a^x = b，那麼可以取以 a 為底數的對數，即 log_a b = x。因此，原方程的解為 x = log_a b。

取對數：如果無法直接將指數方程轉化為對數方程，可以嘗試在兩邊同時取對數。對於正實數 a 和 b，有 log(a^x) = x log a = log b。因此，原方程可以轉化為 x = log b / log a。

需要注意的是，在使用對數法和取對數方法時，需要檢查所得的解是否在定義域內。因為指數函數的定義域為實數集 R，但有些指數方程的解可能不在定義域內，此時需要排除這些無效解。

解方程例子

例子1：解方程 2^x = 8。

應用對數法，取以 2 為底數的對數，得到 x = log_2 8 = 3。

因此，方程 2^x = 8 的解為 x = 3。

例子2：解方程 4^(x+1) = 16^x。

應用對數法，取以 4 為底數的對數，得到 x + 1 = log_4 (16^x) = 2x log_4 2，因此 x = log_4 2。

因此，方程 4^(x+1) = 16^x 的解為 x = log_4 2 ≈ 0.5。需要注意的是，這個解只在定義域內當 4^(x+1) ≠ 0，即 x ≠ -1。

如果大家有什麼補習問題，如私人補習、網上補習好唔好，歡迎你可以隨時再跟我多交流一下，可以Follow 「學博教育中心 Learn Smart Education」 Facebook page同IG得到更多補習課程資訊，亦都可以上我們的補習網頁了解更多!