More about Equations 續方程
解方程是高中數學中重要的一個概念,它在許多不同的領域都有廣泛的應用。從求解物理問題到解決工程問題,方程都扮演了重要的角色。在這個數學概念中,我們學習如何解決不同類型的方程,以及掌握使用不同的方法,如代入法和消元法,來解決這些方程。在本文中,我們將延伸討論如何解決各種類型的方程,包括一元二次方程、分式方程、指數方程、對數方程和三角方程等。透過學習這些技能,我們不僅可以在數學學科中更好地理解和解決問題,更能夠應用這些知識來解決實際問題。
運用圖解法解二元一次方程組和二元二次方程組
use the graphical method to solve simultaneous
equations in two unknowns, one linear and one
quadratic
以下是運用圖解法解二元一次方程組和二元二次方程組的步驟和示意圖:
- 二元一次方程組:假設有以下二元一次方程組:
2x + y = 4
x – y = 1將這兩個方程式表示成直線的形式,如下圖所示:
從圖中可以看出,這兩條直線在 (5/3, 2/3) 的交點處相交,因此 x = 5/3, y = 2/3 為此方程組的解。
- 二元二次方程組:假設有以下二元二次方程組:
y = x^2-8x+14
y = x將兩個方程式表示成標準的二元二次方程形式:
y = x^2 – 8x + 14
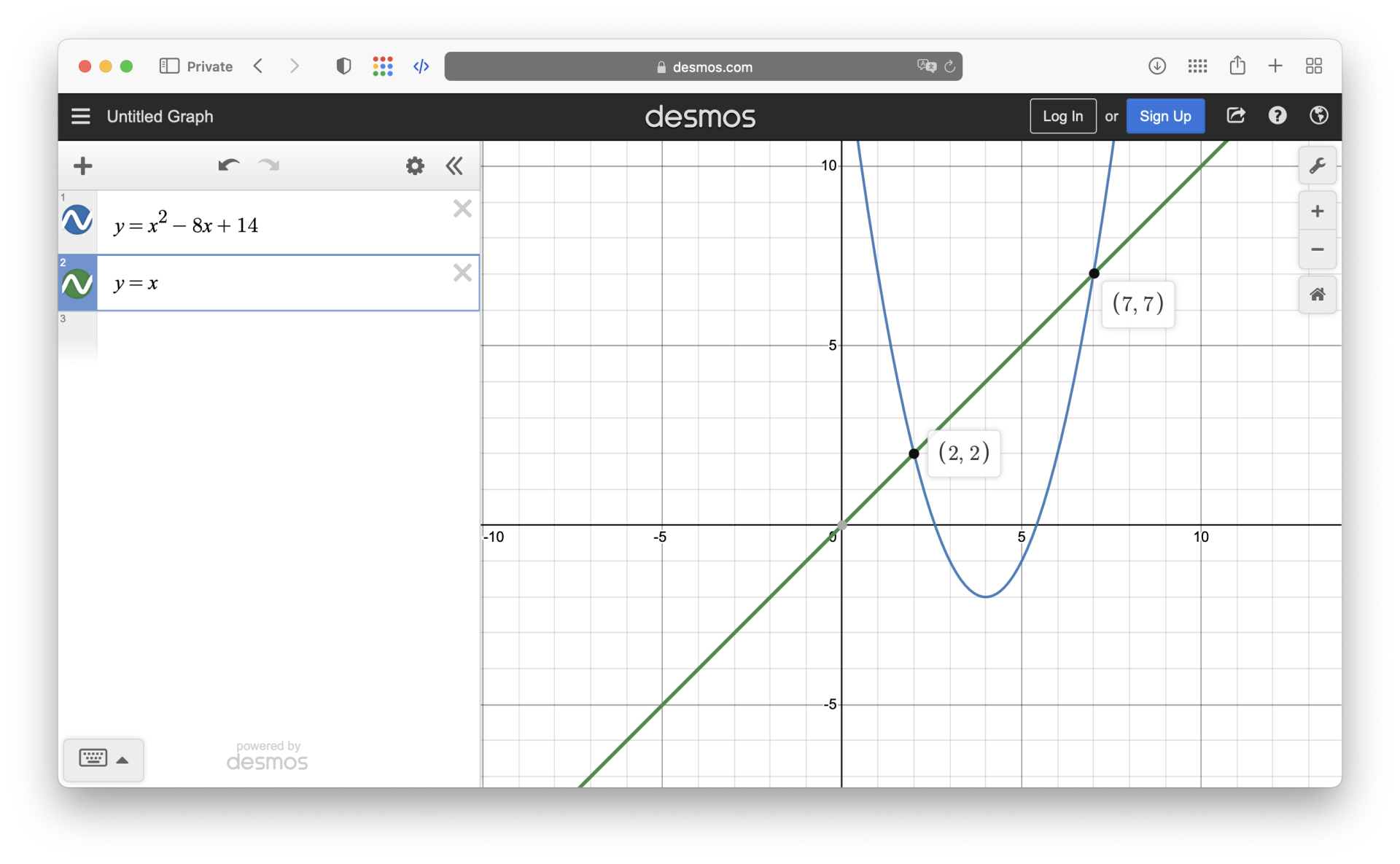
y = x將這兩個方程式表示成二次曲線和直線的形式,如下圖所示:
從圖中可以看出,這條直線和二次曲線在兩個交點處相交,因此我們需要求出這兩個交點的座標。解出 x = 2 和 x = 7,將這兩個值代入 y = x 中,得到:
y = 2 和 y = 7
因此,此方程組的解為 (2, 2) 和 (7, 7)。
以上就是運用圖解法解二元一次方程組和二元二次方程組的步驟和示意圖。
運用代數方法解分別為二元一次及二元二次的聯立方程
use the algebraic method to solve simultaneous
equations in two unknowns, one linear and one
quadratic
- 二元一次方程組:假設有以下二元一次方程組:
x + y = 5
2x – y = 1我們可以使用消元法來求解這個方程組。將第一個方程式兩邊同乘以 2,得到:
2x + 2y = 10
將這個式子和第二個方程式相減,得到:
-3y = -9
解出 y = 3,將這個值代入任意一個方程式中,例如第一個方程式,得到:
x + 3 = 5
解出 x = 2。
因此,此方程組的解為 x = 2, y = 3。
- 二元二次方程組:假設有以下二元二次方程組:
x^2 + y^2 = 9
y = x – 3我們可以將第二個方程式中的 y 代入第一個方程式中,得到:
x^2 + (x – 3)^2 = 9
化簡後得到:
2x^2 – 6x = 0
解出 x = 0或3,將這兩個值代入第二個方程式中,得到:
當 y = 0 – 3 = -3
當 y = 3 – 3 = 0因此,此方程組的解為 (0, -3) 和 (3, 0)。
解可變換為二次方程的方程(其中包括 分
式方程、指數方程、對數方程和三角方程)
solve equations (including fractional equations,
exponential equations, logarithmic equations and
trigonometric equations) which can be transformed
into quadratic equations
以下是解可變換為二次方程的方程的步驟:
- 分式方程:假設有以下分式方程:
(x + 1)/(x – 2) = 2
我們可以先將方程式化簡,得到:
x + 1 = 2(x – 2)
化簡後得到:
x – 5 = 0
解出 x = 5,將這個值代入原方程式中,檢查是否符合原方程式的限制條件,即分母不為零,得到:
(5 + 1)/(5 – 2) = 2
此方程式的解為 x = 5。
然而,如果我們不能將分式方程化簡為線性方程,則可以將分子和分母乘上相同的多項式,將方程式變形為二次方程。
- 指數方程:假設有以下指數方程:
2^(2x + 1) = 16
我們可以先將方程式化簡,得到:
2^(2x + 1) = 2^4
化簡後得到:
2x + 1 = 4
解出 x = 3/2,將這個值代入原方程式中,檢查是否符合原方程式的限制條件,得到:
2^(2(3/2) + 1) = 16
此方程式的解為 x = 3/2。
然而,如果指數方程無法簡化,可以將方程式變形為二次方程,例如將方程式兩邊取對數,得到:
(2x + 1)log2 = log16
再將對數化簡,得到:
2x + 1 = 4
解出 x = 3/2。
- 對數方程:假設有以下對數方程:
log(x + 1) + log(x – 2) = 1
我們可以先將方程式化簡,得到:
log((x + 1)(x – 2)) = 1
化簡後得到:
(x + 1)(x – 2) = 10
將這個式子變形為二次方程,得到:
x^2 – x – 12 = 0
解出 x = 4 和 x = -3,將這兩個值代入原方程式中,檢查是否符合原方程式的限制條件,即對數的底數和參數必須大於零,得到:
log(5) + log(2) = 1
log(-2) + log(-5) = undefined因此,此方程式的解為 x = 4。
- 三角方程:假設有以下三角方程:
2sin^2(x) – 3sin(x) + 1 = 0
我們可以將 sin(x) 看作一個未知數,將方程式變形為二次方程,得到:
2t^2 – 3t + 1 = 0 (其中 t = sin(x))
解出 t = 1 和 t = 1/2,將這兩個值代入原方程式中,檢查是否符合原方程式的限制條件,即 -1 ≤ sin(x) ≤ 1,得到:
sin(x) = 1 (當 t = 1 時)
sin(x) = 1/2 (當 t = 1/2 時)解出 x = 90度 或 x = 30度
解涉及可變換為二次方程的方程之應用題
solve problems involving equations which can be
transformed into quadratic equations
以下是一個應用二次方程的例子:
例題:一個園藝家種了一片長方形的花園,其中一邊比另一邊長 5 英尺,園藝家總共使用了 84 平方英尺的土地。求花園的長和寬分別是多少英尺。
解法:我們可以先設花園的寬為 x 英尺,因為長方形的一邊比另一邊長 5 英尺,所以花園的長為 x + 5 英尺。根據題目所述,花園的面積為 84 平方英尺,因此可以列出以下方程式:
x(x + 5) = 84
將這個式子化簡,得到:
x^2 + 5x – 84 = 0
這是一個二次方程,可以使用求根公式求解,得到:
x = 7或-12
因為花園的寬度必須是正數,所以我們可以排除 x = -12 這個根。因此,花園的寬度為:
x = 7 英尺
花園的長度為:
x + 5 = 12英尺
因此,花園的長和寬分別是 12 英尺和7 英尺。
如果大家有什麼補習問題,如私人補習、網上補習好唔好,歡迎你可以隨時再跟我多交流一下,可以Follow 「學博教育中心 Learn Smart Education」 Facebook page同IG得到更多補習課程資訊,亦都可以上我們的補習網頁了解更多!
DSE 數學 文章系列
- Quadratic Equation in One Unknown 一元二次方程
- Functions and Graphs 函數及其圖像
- Equations of Straight Lines 直線方程
- More about Polynomials 續多項式
- Exponential Functions 指數函數
- Logarithmic Functions 對數函數
- More about Equations 續方程
- Variations 變分
- More about Trigonometry 續三角學
- Basic Properties of Circles 圓的基本性質
- Tangents to Circles 圓形切線
- Inequalities 不等式
- Linear Programming 線性規畫
- Applications of Trigonometry in 2-dimensional Problems 二維三角學應用
- Applications of Trigonometry in 3-dimensional Problems 三維三角學應用
- Equations of Circles 圓方程
- Locus 軌跡
- Measures of Dispersion 離差的度量
- Permutation and Combination 排列與組合
- More about Probability 續概率
- ASGS 等差數列與等比數列
- Uses and Abuses of Statistics 統計的應用及誤用




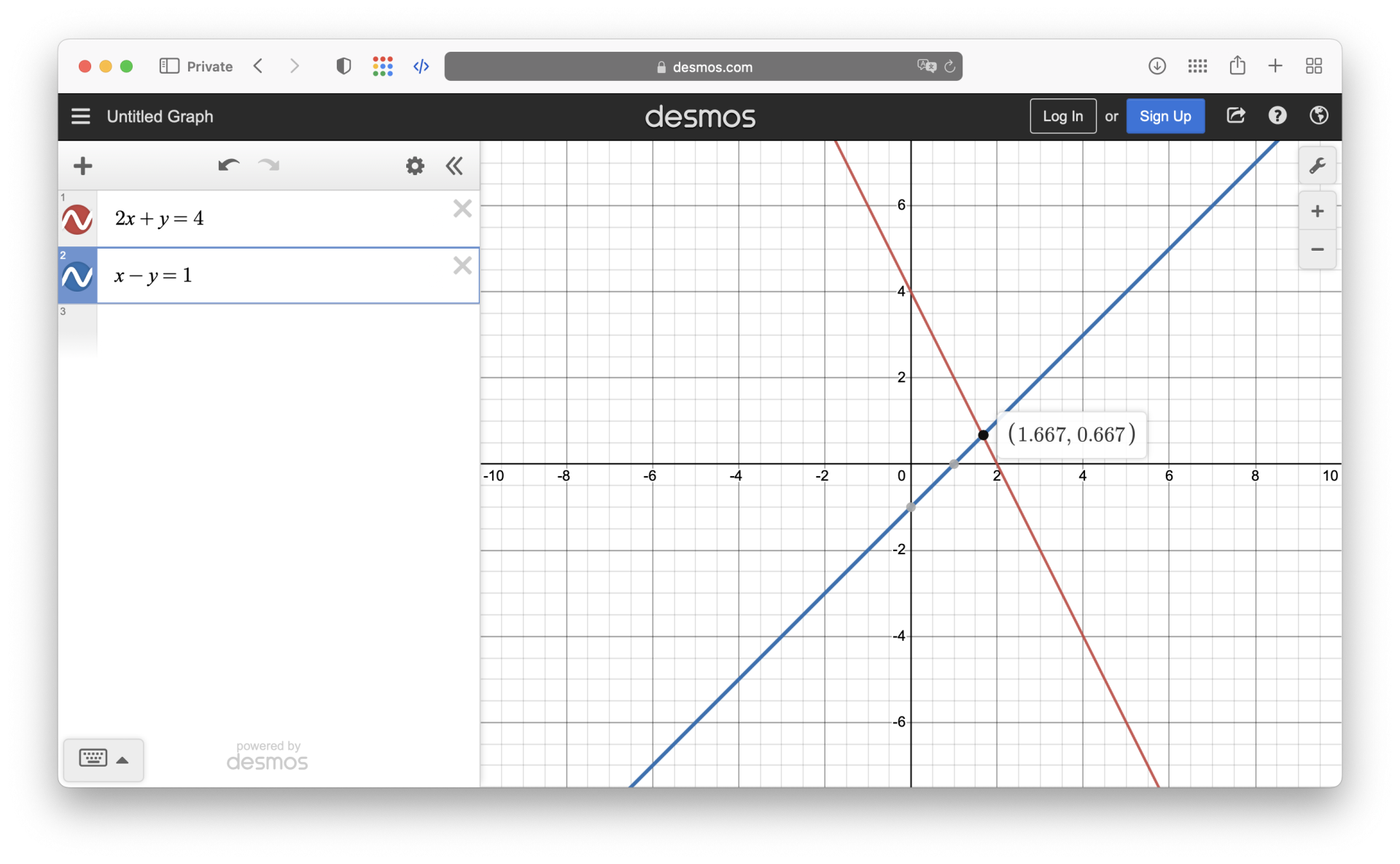 從圖中可以看出,這兩條直線在 (5/3, 2/3) 的交點處相交,因此 x = 5/3, y = 2/3 為此方程組的解。
從圖中可以看出,這兩條直線在 (5/3, 2/3) 的交點處相交,因此 x = 5/3, y = 2/3 為此方程組的解。